Weekly Report [5]

Jinning, 08/07/2018

Try validation on training set

The result:

ips: 110.97455105041419511

ips_std: 5.6860887585293482787

I wonder why it gets so large IPS?

Because repetition of training data?

I count the impressions having the same features, such as:

{'f': '[0, 9, 10, 11, 12, 19, 112, 226, 227, 230, 234, 272, 273, 958, 959, 960]', 'id': 50543898}
{'f': '[0, 9, 10, 11, 12, 19, 112, 226, 227, 230, 234, 272, 273, 958, 959, 960]', 'id': 6042332}
{'f': '[0, 9, 10, 11, 12, 19, 112, 226, 227, 230, 234, 272, 273, 958, 959, 960]', 'id': 5226873}
{'f': '[0, 9, 10, 11, 12, 19, 112, 226, 227, 230, 234, 272, 273, 958, 959, 960]', 'id': 10376281}
{'f': '[0, 9, 10, 11, 12, 19, 112, 226, 227, 234, 272, 273, 958, 959, 960, 7705]', 'id': 2646568}
{'f': '[0, 9, 10, 11, 12, 19, 112, 226, 227, 234, 272, 273, 958, 959, 960, 7705]', 'id': 4875183}
{'f': '[0, 9, 10, 11, 12, 19, 226, 227, 230, 231, 234, 272, 273, 958, 959, 960]', 'id': 7945582}
{'f': '[0, 9, 10, 11, 12, 19, 226, 227, 230, 231, 234, 272, 273, 958, 959, 960]', 'id': 12753081}
{'f': '[0, 9, 10, 11, 12, 19, 190, 723, 730, 904, 958, 959, 1673, 1674, 1675, 1676]', 'id': 30292516}
{'f': '[0, 9, 10, 11, 12, 19, 190, 723, 730, 904, 958, 959, 1673, 1674, 1675, 1676]', 'id': 28541751}
...

There are 5399483 impressions are repeated.

There are about 14100000 impressions in total.

So the repetition is about 38.3% impressions being repeated.

The largest repetition for a same feature is 35228.

Maybe we should clean the training set.

Adding current policy into the weighting of loss

1. Not building computational graph of \(\pi_w\)

Loss: \(\frac{\tilde{\pi}}{\pi_0}\left[ y \cdot \log \sigma(x) + (1 - y) \cdot \log (1 - \sigma(x)) \right]\)

Get a result of IPS=52, IPS_std=5 on CrowdAI test.

2. Building calculation of \(\pi_w\)

Loss: \(\frac{\tilde{\pi}(w)}{\pi_0}\left[ y \cdot \log \sigma(x) + (1 - y) \cdot \log (1 - \sigma(x)) \right]\)

The program is running:

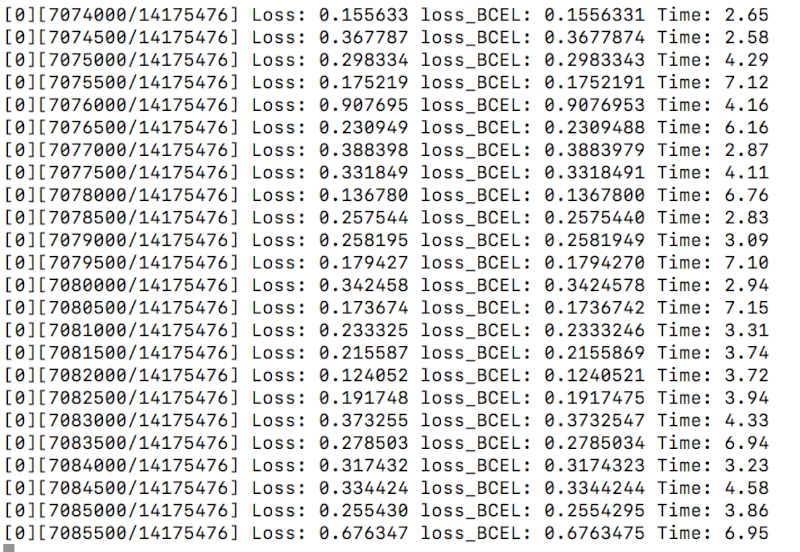
The loss decreases. However, the loss can vary distinctly.

• batchSize too small
• model unstable

2. Building calculation of \(\pi_w\). Adding propensity loss

Loss: \(\frac{\tilde{\pi}(w)}{\pi_0}\left[ y \cdot \log \sigma(x) + (1 - y) \cdot \log (1 - \sigma(x)) \right] + (tanh^2(\frac{1}{\tilde{\pi}(w)})-tanh^2(\frac{1}{\pi_0}))^{\frac{1}{2}}\)

The program is running: